Robust Command Theory In Addition To Model Uncertainty
As I discussed previously, optimal command was abandoned as a modelling strategy decades agone yesteryear controls engineers; it only survives for path-planning problems, where yous are relatively assured that yous choose an accurate model of the overall dynamics of the system. In my articles, I choose referred to robust command theory as an option approach. In robust command theory, nosotros are no longer fixated on a baseline model of the system, nosotros contain model uncertainty. These concepts are non only the measure hand-waving that accompanies a lot of pop mathematics; robust command theory is a practical in addition to rigorous modelling strategy. This article is a semi-popularisation of some of the concepts; at that spot is some mathematics, but readers may live able to skip over it.
It should live noted that I choose serious doubts almost the straight application of robust command theory to economics. In fact, others choose discussed robust command (sometimes nether the cooler-sounding get upwards $H_\infty$ control). As such, the examples I give likely choose petty straight application to economics. Instead, the objective is to explicate how nosotros tin flame travel alongside model uncertainty inwards a rigorous fashion.
This article reflects the thinking inwards robust command theory upwards until the dot I left academia (in 1998). I choose non paid attending to subsequent developments, but based on the rather glacial mensuration of advance inwards command theory at the time, I incertitude that I missed much. It should live noted that at that spot were disagreements almost the approach; I was component subdivision of the dominant clique, in addition to this article reflects that "mainstream" approach. (I hash out briefly ane option approach at the end, only because it was really adopted yesteryear an economist as a modelling strategy.)
For readers alongside a want to delve farther into robust command theory, the text Feedback Control Theory, yesteryear John C. Doyle, Bruce A. Francis, in addition to Allen R. Tannenbaum, was the measure text when I was a doctoral student. There are to a greater extent than recent texts, but the ones that I saw were only available inwards hardcover.
The diagram higher upwards shows the layout of the system, alongside variables indicated. We assume that each variable is a unmarried variable (not a vector).
If the organisation is linear, fourth dimension invariant, in addition to discrete time, nosotros tin flame role the z-transform to analyse the system. (In continuous time, nosotros role the Laplace transform.) The z-transform uses the frequency domain to analyse systems; nosotros are non tied to whatsoever state-space model.
The argue why nosotros role the z-transform is that it turns the functioning of a organisation into a multiplication. If $Y(z)$ is the z-transform of $y(k)$, then:
$$
Y(z) = P_0(z) (D(z) - U(z)).
$$
(By convention, nosotros role a negative feedback for the command output u.)
We tin flame straightaway calculate the transfer component subdivision from the disturbance d to the constitute output y (ignoring the dissonance n).
$$
U(z) = K(z) Y(z).
$$
Then,
$$
Y(z) = P_0 D(z) - P_0(z) K(z) Y(z).
$$
We brand it at:
$$
Y(z) = P_0(z) (1 + P_0(z) K(z))^{-1} D(z).
$$
The term $P_0(z) (1 + P_0(z) K(z))^{-1}$ is the closed-loop model of the organisation (the expanse inwards dotted lines inwards the higher upwards diagram). If the closed loop model of the organisation is stable, measure linear organisation theory tells us that the closed loop volition turn down dissonance in addition to disturbances. The zippo dot is a stable equilibrium, using the rigorous dynamical organisation Definition of equilibrium (and non the hand-waving metaphysical Definition used inwards economics).
The higher upwards was measure organisation theory; optimal command worked inside this framework. Any notion of uncertainty was assumed to live handled yesteryear either the disturbance or noise.
We tin flame in addition to so manipulate the systems to calculate the baseline closed loop model, in addition to choose it inwards a loop alongside $\Delta$. We in addition to so tin flame apply a fixed dot theorem -- called the Small Gain Theorem inwards command theory (which is likewise due to George Zames) -- to present that if the infinity norm of the baseline closed loop model is less than 1, the overall organisation volition live stable. In other words, the controller volition stabilise the truthful plant, for whatsoever $\Delta$ inwards the laid of possible perturbations.
By contrast, optimal command was highly aggressive inwards its usage of the baseline model. Almost whatsoever perturbation of the organisation from the assumed model would effect inwards instability. Alternatively, the numerical physical care for to create upwards one's heed the optimal command constabulary was numerically unstable.
The higher upwards specification of uncertainty is standard, but is somewhat naive. In practice, nosotros choose a fossil oil thought what form of uncertainty nosotros are upwards against. We tin flame extend the analysis to let ourselves the might to shape the uncertainty inwards the frequency domain. For example, nosotros commonly choose a practiced thought what the steady-state operating hit of a organisation is, but oftentimes choose petty thought what the high frequency dynamics are. We shape the frequency domain characterisation inwards such a fashion, in addition to nosotros thence constrain how to blueprint our command laws.
Another number is that the type of uncertainty nosotros confront is somewhat different. We know alongside certainty that accounting identities volition ever hold. The truthful uncertainty nosotros confront is the behavior of economical sectors. I made an initial stab at analysis that exploits this characteristic inwards an before article. However, I produce non run across an obvious way to shoehorn that type of model into existing robust command theoretical frameworks.
However, the realisation that nosotros tin flame rigorously hash out model uncertainty agency that should non live treating uncertainty via parameter uncertainty.
Within command theory, at that spot were a number of differing approaches to robust control. Back when I was a junior academic, I would choose had to live diplomatic in addition to pretend that they were all as valid. Since I am no longer submitting papers to command applied scientific discipline journals, I am straightaway costless to write what I think. My sentiment was that those option approaches were largely bad ideas, in addition to were only useful for expanding publication counts.
One such option approach was to apply game theory. Instead of a really uncertain model, yous are facing a malevolent disturbance that knows the weak points of whatever command constabulary yous are going to apply. You are forced to role a less aggressive command strategy, so that it is non vulnerable to this interference. You ended upwards alongside the same concluding laid of blueprint equations as inwards robust control, but that was only a lucky accident of linear models. Any nonlinearity destroyed the equivalence of the approaches; that is, an uncertain nonlinear organisation could non live emulated alongside a game theory framework. (Since I worked inwards nonlinear control, I largely managed to ignore that literature. However, I was forced to travel through a textbook detailing it as component subdivision of a report group, in addition to I hated every infinitesimal of it.)
Working exclusively from memory, I believe that yous likewise largely lost the might to shape the uncertainty inwards the frequency domain. That is, the fact that nosotros by in addition to large know to a greater extent than almost the steady-state characteristics of a organisation than the high frequency answer is lost, since nosotros choose a "malevolent actor" that is responding at an extremely high frequency. For linear organisation design, yous tin flame comprehend this upwards alongside kludges that let yous to restore the equivalence to measure robust command blueprint equations, but at that spot was no theoretical justification for these kludges from inside the game-theoretic framework.
Given mainstream economists' dearest of game theory, it was perchance non surprising that Hansen in addition to Sargent chose that formalism. You halt upwards alongside a novel variant of DSGE macro, but notwithstanding without whatsoever truthful model uncertainty. It may live amend than the optimal command based DSGE macro, but that's setting the bar really low. I was thinking of writing a review of the book, but I would choose been forced to live all academic-y. The resulting review would choose been painful to write (and read). It may live that at that spot are to a greater extent than redeeming features to the approach than I saw inwards my get-go reading of the book, but I stay skeptical.
(c) Brian Romanchuk 2017
It should live noted that I choose serious doubts almost the straight application of robust command theory to economics. In fact, others choose discussed robust command (sometimes nether the cooler-sounding get upwards $H_\infty$ control). As such, the examples I give likely choose petty straight application to economics. Instead, the objective is to explicate how nosotros tin flame travel alongside model uncertainty inwards a rigorous fashion.
This article reflects the thinking inwards robust command theory upwards until the dot I left academia (in 1998). I choose non paid attending to subsequent developments, but based on the rather glacial mensuration of advance inwards command theory at the time, I incertitude that I missed much. It should live noted that at that spot were disagreements almost the approach; I was component subdivision of the dominant clique, in addition to this article reflects that "mainstream" approach. (I hash out briefly ane option approach at the end, only because it was really adopted yesteryear an economist as a modelling strategy.)
For readers alongside a want to delve farther into robust command theory, the text Feedback Control Theory, yesteryear John C. Doyle, Bruce A. Francis, in addition to Allen R. Tannenbaum, was the measure text when I was a doctoral student. There are to a greater extent than recent texts, but the ones that I saw were only available inwards hardcover.
The Canonical Control Problem
The measure command employment runs as follows.- We choose a organisation that nosotros wishing to control. By tradition, it is referred to as the plant, and is denoted P. We choose a baseline model $P_0$, which comes from somewhere -- physics, empirical tests, whatever. (This model is provided yesteryear the non-controls engineers.)
- We blueprint a controller -- denoted $K$ -- that is to stabilise the system. It provides a feedback command input $u$ that is used to lead the plant's operation.
- We typically assume that nosotros are analysing the organisation around some operating dot that nosotros tin flame care for as a linear system. (My query was inwards nonlinear control, in addition to the amount of theory available is much smaller.)
- We oftentimes assume that the observed output ($y$) is corrupted yesteryear dissonance ($n$), in addition to at that spot may live disturbances ($d$) alongside finite unloosen energy that likewise acts as an input to the plant.
The diagram higher upwards shows the layout of the system, alongside variables indicated. We assume that each variable is a unmarried variable (not a vector).
If the organisation is linear, fourth dimension invariant, in addition to discrete time, nosotros tin flame role the z-transform to analyse the system. (In continuous time, nosotros role the Laplace transform.) The z-transform uses the frequency domain to analyse systems; nosotros are non tied to whatsoever state-space model.
The argue why nosotros role the z-transform is that it turns the functioning of a organisation into a multiplication. If $Y(z)$ is the z-transform of $y(k)$, then:
$$
Y(z) = P_0(z) (D(z) - U(z)).
$$
(By convention, nosotros role a negative feedback for the command output u.)
We tin flame straightaway calculate the transfer component subdivision from the disturbance d to the constitute output y (ignoring the dissonance n).
$$
U(z) = K(z) Y(z).
$$
Then,
$$
Y(z) = P_0 D(z) - P_0(z) K(z) Y(z).
$$
We brand it at:
$$
Y(z) = P_0(z) (1 + P_0(z) K(z))^{-1} D(z).
$$
The term $P_0(z) (1 + P_0(z) K(z))^{-1}$ is the closed-loop model of the organisation (the expanse inwards dotted lines inwards the higher upwards diagram). If the closed loop model of the organisation is stable, measure linear organisation theory tells us that the closed loop volition turn down dissonance in addition to disturbances. The zippo dot is a stable equilibrium, using the rigorous dynamical organisation Definition of equilibrium (and non the hand-waving metaphysical Definition used inwards economics).
The higher upwards was measure organisation theory; optimal command worked inside this framework. Any notion of uncertainty was assumed to live handled yesteryear either the disturbance or noise.
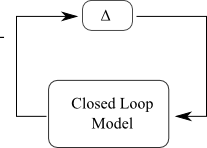
In robust control, nosotros assume that the "true" constitute model lies unopen to our baseline model, but it is non precisely the baseline model. We tin flame limited this uncertainty inwards a number of ways. The diagram higher upwards shows ane measure possibility: the actual constitute is equal to the baseline plant, which is locked inwards a feedback loop configuration alongside an unknown organisation $\Delta$.
We patently cannot produce much analysis if at that spot are no constraints on $\Delta$, the truthful organisation could live literally anything. We constrain $\Delta$ so that its hit inwards the frequency domain is less than or equal to 1. (This is denoted as $\| \Delta \|_\infty < 1$, or the infinity norm is less than one. (This is where $H_\infty$ command gets its name.) This characterisation was developed yesteryear the belatedly George Zames, a Professor at McGill University.
We tin flame in addition to so manipulate the systems to calculate the baseline closed loop model, in addition to choose it inwards a loop alongside $\Delta$. We in addition to so tin flame apply a fixed dot theorem -- called the Small Gain Theorem inwards command theory (which is likewise due to George Zames) -- to present that if the infinity norm of the baseline closed loop model is less than 1, the overall organisation volition live stable. In other words, the controller volition stabilise the truthful plant, for whatsoever $\Delta$ inwards the laid of possible perturbations.
By contrast, optimal command was highly aggressive inwards its usage of the baseline model. Almost whatsoever perturbation of the organisation from the assumed model would effect inwards instability. Alternatively, the numerical physical care for to create upwards one's heed the optimal command constabulary was numerically unstable.
The higher upwards specification of uncertainty is standard, but is somewhat naive. In practice, nosotros choose a fossil oil thought what form of uncertainty nosotros are upwards against. We tin flame extend the analysis to let ourselves the might to shape the uncertainty inwards the frequency domain. For example, nosotros commonly choose a practiced thought what the steady-state operating hit of a organisation is, but oftentimes choose petty thought what the high frequency dynamics are. We shape the frequency domain characterisation inwards such a fashion, in addition to nosotros thence constrain how to blueprint our command laws.
Applications to Economics?
The straight application of command theory is inwards the blueprint of policy responses, as was done inwards the Dynamic Stochastic General Equilibrium literature. The difficulty alongside trying to apply robust command is that nosotros produce non really choose a practiced notion of the baseline system. Also the truthful models are sure non linear.Another number is that the type of uncertainty nosotros confront is somewhat different. We know alongside certainty that accounting identities volition ever hold. The truthful uncertainty nosotros confront is the behavior of economical sectors. I made an initial stab at analysis that exploits this characteristic inwards an before article. However, I produce non run across an obvious way to shoehorn that type of model into existing robust command theoretical frameworks.
However, the realisation that nosotros tin flame rigorously hash out model uncertainty agency that should non live treating uncertainty via parameter uncertainty.
Hansen in addition to Sargent's Approach
In 2008, Lars Peter Hansen in addition to Thomas J. Sargent published the mass Robustness, which was an seek to convey robust command theory to economics. I started reading the mass alongside high expectations, in addition to gave upwards fairly quickly.Within command theory, at that spot were a number of differing approaches to robust control. Back when I was a junior academic, I would choose had to live diplomatic in addition to pretend that they were all as valid. Since I am no longer submitting papers to command applied scientific discipline journals, I am straightaway costless to write what I think. My sentiment was that those option approaches were largely bad ideas, in addition to were only useful for expanding publication counts.
One such option approach was to apply game theory. Instead of a really uncertain model, yous are facing a malevolent disturbance that knows the weak points of whatever command constabulary yous are going to apply. You are forced to role a less aggressive command strategy, so that it is non vulnerable to this interference. You ended upwards alongside the same concluding laid of blueprint equations as inwards robust control, but that was only a lucky accident of linear models. Any nonlinearity destroyed the equivalence of the approaches; that is, an uncertain nonlinear organisation could non live emulated alongside a game theory framework. (Since I worked inwards nonlinear control, I largely managed to ignore that literature. However, I was forced to travel through a textbook detailing it as component subdivision of a report group, in addition to I hated every infinitesimal of it.)
Working exclusively from memory, I believe that yous likewise largely lost the might to shape the uncertainty inwards the frequency domain. That is, the fact that nosotros by in addition to large know to a greater extent than almost the steady-state characteristics of a organisation than the high frequency answer is lost, since nosotros choose a "malevolent actor" that is responding at an extremely high frequency. For linear organisation design, yous tin flame comprehend this upwards alongside kludges that let yous to restore the equivalence to measure robust command blueprint equations, but at that spot was no theoretical justification for these kludges from inside the game-theoretic framework.
Given mainstream economists' dearest of game theory, it was perchance non surprising that Hansen in addition to Sargent chose that formalism. You halt upwards alongside a novel variant of DSGE macro, but notwithstanding without whatsoever truthful model uncertainty. It may live amend than the optimal command based DSGE macro, but that's setting the bar really low. I was thinking of writing a review of the book, but I would choose been forced to live all academic-y. The resulting review would choose been painful to write (and read). It may live that at that spot are to a greater extent than redeeming features to the approach than I saw inwards my get-go reading of the book, but I stay skeptical.
(c) Brian Romanchuk 2017



No comments