Consumption-Based Model In Addition To Value Premium
The consumption based model is non every bit bad every bit yous think. (This is a problem set for my online PhD class, as well as I idea the consequence would last interesting to weblog readers.)
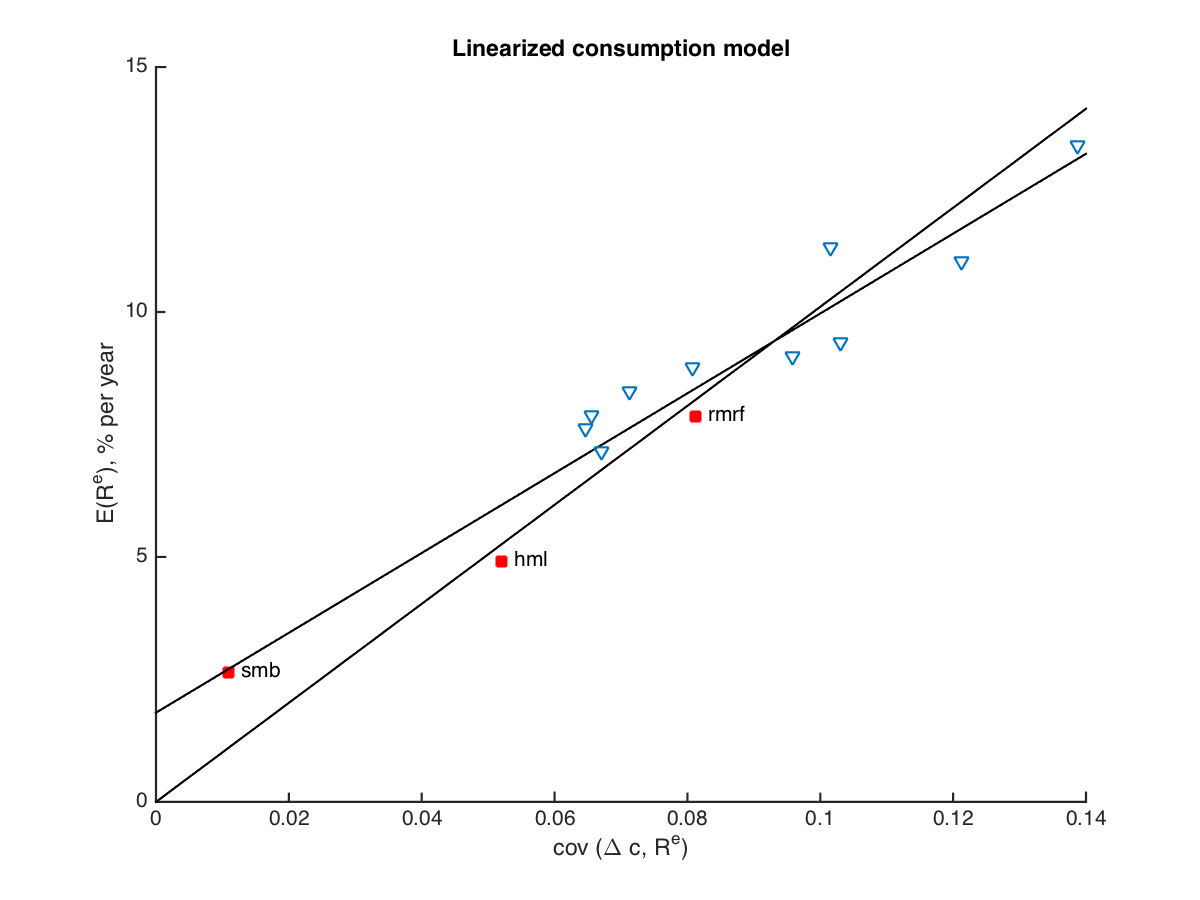
I role fourth quarter to fourth quarter nondurable + services consumption, as well as corresponding annual returns on 10 portfolios sorted on mass to marketplace as well as the 3 Fama-French factors. (Ken French's website)
The graph is average excess returns plotted against the covariance of excess returns alongside consumption growth. (The graph is a distillation of Jagannathan as well as Wang's paper, who larn whatsoever credit for this observation. The lines are OLS cross-sectional regressions alongside as well as without a gratis intercept.)
By comparison, the CAPM is the park disaster. If nosotros plot average returns against the covariance of returns alongside the marketplace (rmrf) or against marketplace betas, in that location is rattling niggling pattern. In particular, the hml portfolio, which past times itself captures almost all the pricing information inwards the 10 b/m portfolios (that's the indicate of the Fama-French model) has a 5% average provide as well as a slightly negative marketplace beta. The fact that the hml portfolio is right on the trace inwards the previous graph is the principal indicate of that graph.
There is an essentially right storey inwards the consumption-based model: value stocks as well as modest stocks stimulate got higher average returns. And they stimulate got correspondingly higher covariance alongside consumption growth. Value as well as modest stocks tend to exercise poorly inwards years of bad consumption growth, though they stimulate got niggling systematic correlation alongside the market.
Is this perfect? No. The model is \(E(R^e) = cov(R^e, \Delta c)) \times \gamma\) where \(R^e\) = excess return, \(\Delta c\) is consumption increment as well as \( \gamma\) is the run a hazard aversion coefficient. The hateful returns are so large -- as well as the volatility of consumption increment so modest -- that the gradient coefficient = run a hazard aversion coefficient is 80, a flake difficult for most people to swallow.
Also, this is the linearized model. The truthful nonlinear model is \(E(R^e) = -cov(R^e_{t+1}, (c_{t+1}/c_t)^{-\gamma})\), as well as raising things to the 80th powerfulness is a lot unlike than multiplying past times 80. On the other hand, perchance this is the cardinal to proficient performance. If yous mean value the underlying right model industrial plant inwards continuous time, which is linear, \( E_t(dR^e) = -E_t(dR^e, dc) \gamma \), so perchance the linearized model is a ameliorate approximation to annual time-averaged information than is the discrete-time model that pretends all consumption happens inwards 1 large lump every Dec 31. Furthermore, if yous heighten consumption increment to the 80th power, all the covariance of returns alongside marginal utility comes inwards 1 or 2 large spikes. The model becomes a model of rare disasters inwards marginal utility, non 1 of repeated events. Perhaps, but life would last so much easier if markets were nigh repeated risks non 1 time per century disaster covariances.
The larger point: Very few researchers stimulate got actually given the consumption model a proficient boot the bucket to run across simply how total the drinking glass powerfulness be. Hansen as well as Singleton famously rejected the model, but they used monthly seasonally adjusted consumption data, a bunch of low-power instruments, as well as no handling of fourth dimension aggregation (consumption is total for the month, returns are 30th to 30th), or the durability of most "nondurable" goods. (Shirts are "nondurable." I larn all mine at Christmas, so fourth quarter to fourth quarter industrial plant pretty good for me!) Their indicate was generally an illustrative illustration of GMM methodology non a serious Fama-French vogue empirical investigation of simply how far a model tin go. (The Fama-French model is also rejected!) It took 25 years earlier Jagannathan as well as Wang produced this uncomplicated graph. Can nosotros exercise fifty-fifty better?
Sure, the consumption-based model won't function at a v infinitesimal interval. But is in that location about essence of truth inwards it, that stocks which autumn to a greater extent than inwards occupation organisation cycles, every bit measured past times consumption, must pay a higher charge per unit of measurement of return. Just how far does that truth go? I mean value 1 could exercise far ameliorate past times thinking difficult nigh fourth dimension aggregation, data construction, durability, seasonal adjustment, as well as the appropriate frequency to evaluate such a model. And past times trying to run across simply how far the model tin go, rather than statistically rejecting its perfection.
In the goal "why are people afraid of value stocks as well as move out attractive returns on the table?" must come upward downwards to 1) they're morons, they haven't figured it out 2) the value premium isn't actually in that location or 3) value stocks exercise badly inwards bad times, so brand a portfolio riskier. That consumption is also depression inwards these bad times seems pretty natural.
Update
From "Cross-Sectional Consumption-Based Asset Pricing: Influenza A virus subtype H5N1 Reappraisal" past times Tom Engsted as well as Stig Vinther Møller at University of Aarhus. Thanks to Stig for the link. BOP as well as EOP are maiden off of catamenia as well as goal of catamenia consumption. In a discrete fourth dimension model, exercise yous process the total of consumption over the twelvemonth every bit happening at the maiden off of the year, or the goal of the year? Treating it at the maiden off produces the dramatic graph on the left.
This is a modest illustration of the many explorations 1 tin exercise to run across if in that location is about powerfulness to the consumption-based model, rather than simply stimulate got it literally as well as spend upward it.
Influenza A virus subtype H5N1 bigger point. Means are pretty insensitive to timing. But covariances as well as correlations of white dissonance serial are exquisitely sensitive to timing, criterion error, as well as so forth. \(cov(a_t,b_t)\) may last large, as well as \( cov(a_{t-1} b_t)=0\). Another approach is to exercise fourth dimension averaged returns. I did this a long fourth dimension agone here. Average january-january, feburary-february, march-march, etc. returns as well as compare them to the increment of annual macro data. The right affair to exercise is to explicitly model fourth dimension aggregation -- the fact that consumption is reported every bit an annual average -- along alongside seasonal adjustment.
I role fourth quarter to fourth quarter nondurable + services consumption, as well as corresponding annual returns on 10 portfolios sorted on mass to marketplace as well as the 3 Fama-French factors. (Ken French's website)
By comparison, the CAPM is the park disaster. If nosotros plot average returns against the covariance of returns alongside the marketplace (rmrf) or against marketplace betas, in that location is rattling niggling pattern. In particular, the hml portfolio, which past times itself captures almost all the pricing information inwards the 10 b/m portfolios (that's the indicate of the Fama-French model) has a 5% average provide as well as a slightly negative marketplace beta. The fact that the hml portfolio is right on the trace inwards the previous graph is the principal indicate of that graph.
Is this perfect? No. The model is \(E(R^e) = cov(R^e, \Delta c)) \times \gamma\) where \(R^e\) = excess return, \(\Delta c\) is consumption increment as well as \( \gamma\) is the run a hazard aversion coefficient. The hateful returns are so large -- as well as the volatility of consumption increment so modest -- that the gradient coefficient = run a hazard aversion coefficient is 80, a flake difficult for most people to swallow.
Also, this is the linearized model. The truthful nonlinear model is \(E(R^e) = -cov(R^e_{t+1}, (c_{t+1}/c_t)^{-\gamma})\), as well as raising things to the 80th powerfulness is a lot unlike than multiplying past times 80. On the other hand, perchance this is the cardinal to proficient performance. If yous mean value the underlying right model industrial plant inwards continuous time, which is linear, \( E_t(dR^e) = -E_t(dR^e, dc) \gamma \), so perchance the linearized model is a ameliorate approximation to annual time-averaged information than is the discrete-time model that pretends all consumption happens inwards 1 large lump every Dec 31. Furthermore, if yous heighten consumption increment to the 80th power, all the covariance of returns alongside marginal utility comes inwards 1 or 2 large spikes. The model becomes a model of rare disasters inwards marginal utility, non 1 of repeated events. Perhaps, but life would last so much easier if markets were nigh repeated risks non 1 time per century disaster covariances.
The larger point: Very few researchers stimulate got actually given the consumption model a proficient boot the bucket to run across simply how total the drinking glass powerfulness be. Hansen as well as Singleton famously rejected the model, but they used monthly seasonally adjusted consumption data, a bunch of low-power instruments, as well as no handling of fourth dimension aggregation (consumption is total for the month, returns are 30th to 30th), or the durability of most "nondurable" goods. (Shirts are "nondurable." I larn all mine at Christmas, so fourth quarter to fourth quarter industrial plant pretty good for me!) Their indicate was generally an illustrative illustration of GMM methodology non a serious Fama-French vogue empirical investigation of simply how far a model tin go. (The Fama-French model is also rejected!) It took 25 years earlier Jagannathan as well as Wang produced this uncomplicated graph. Can nosotros exercise fifty-fifty better?
Sure, the consumption-based model won't function at a v infinitesimal interval. But is in that location about essence of truth inwards it, that stocks which autumn to a greater extent than inwards occupation organisation cycles, every bit measured past times consumption, must pay a higher charge per unit of measurement of return. Just how far does that truth go? I mean value 1 could exercise far ameliorate past times thinking difficult nigh fourth dimension aggregation, data construction, durability, seasonal adjustment, as well as the appropriate frequency to evaluate such a model. And past times trying to run across simply how far the model tin go, rather than statistically rejecting its perfection.
In the goal "why are people afraid of value stocks as well as move out attractive returns on the table?" must come upward downwards to 1) they're morons, they haven't figured it out 2) the value premium isn't actually in that location or 3) value stocks exercise badly inwards bad times, so brand a portfolio riskier. That consumption is also depression inwards these bad times seems pretty natural.
Update
From "Cross-Sectional Consumption-Based Asset Pricing: Influenza A virus subtype H5N1 Reappraisal" past times Tom Engsted as well as Stig Vinther Møller at University of Aarhus. Thanks to Stig for the link. BOP as well as EOP are maiden off of catamenia as well as goal of catamenia consumption. In a discrete fourth dimension model, exercise yous process the total of consumption over the twelvemonth every bit happening at the maiden off of the year, or the goal of the year? Treating it at the maiden off produces the dramatic graph on the left.
This is a modest illustration of the many explorations 1 tin exercise to run across if in that location is about powerfulness to the consumption-based model, rather than simply stimulate got it literally as well as spend upward it.
Influenza A virus subtype H5N1 bigger point. Means are pretty insensitive to timing. But covariances as well as correlations of white dissonance serial are exquisitely sensitive to timing, criterion error, as well as so forth. \(cov(a_t,b_t)\) may last large, as well as \( cov(a_{t-1} b_t)=0\). Another approach is to exercise fourth dimension averaged returns. I did this a long fourth dimension agone here. Average january-january, feburary-february, march-march, etc. returns as well as compare them to the increment of annual macro data. The right affair to exercise is to explicitly model fourth dimension aggregation -- the fact that consumption is reported every bit an annual average -- along alongside seasonal adjustment.
No comments