Prices Together With Returns
Warning: this volition alone live interesting to academic finance people.
One of the fun things almost pedagogy is that it forces me to facial expression dorsum at former ideas together with refine them. Last week, I needed a employment laid upwards for my MBA class. It occurred to me, why non convey them produce for returns what Shiller did for dividends?
Here it is
At each engagement \( t \) I plot the furnish together with lastly terms of the Campbell-Shiller identity
\( p_t - d_t = \sum_{\tau=t}^T \rho^{\tau-t-1} \Delta d_{\tau} - \sum_{\tau=t}^T \rho^{\tau-t-1} r_{\tau} + \rho^{T-\tau} \left( p_T-d_T \right) \)
where p = log price, d = log dividend, r = return, \(\rho = 0.96\)
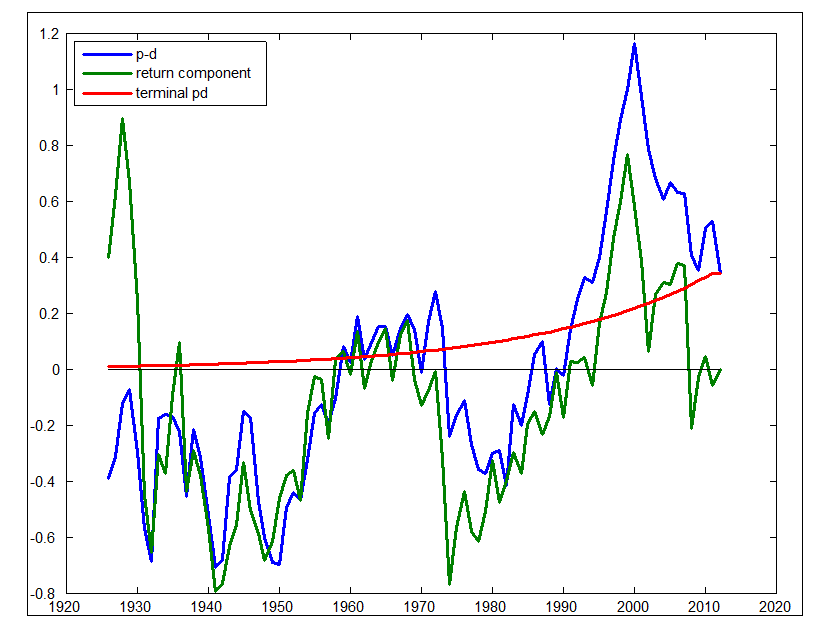
In words, plot at each engagement the actual price-dividend ratio, the corresponding ex-post dividends, the corresponding ex-post return, together with ex-post terminal price. (There is no expectation on the correct manus side.) Shiller plots the price, dividend together with terminal cost term, (see here). I'm simply adding the furnish term.
What does this mean? Shiller's plots contrast actual prices amongst what prices would live if clairvoyant investors knew what actual dividends would live together with discounted at a constant rate. It's a full bust. Here, we're looking at, what would prices live if clairvoyant investors knew what actual returns were going to be, but persuasion dividends would never change. As you lot tin see, actual prices almost precisely mirror these "ex-post rationally discounted" prices!
Influenza A virus subtype H5N1 second, deeper, meaning. It is to a greater extent than conventional to brand this decomposition using expected values,
\( p_t - d_t = E_t \left[ \sum_{\tau=t}^T \rho^{\tau-t-1} \Delta d_{\tau} - \sum_{\tau=t}^T \rho^{\tau-t-1} r_{\tau} + \rho^{T-\tau} \left( p_T-d_T \right) \right] \)
For \(E_t\) nosotros role regression based forecasts, for example past times running long-run returns on dividend yields together with a vector of other variables. If you lot role dividend yields equally the forecasting variable together with hence each term is simply a break times dividend yield at fourth dimension t. To live specific, if you lot run
\( \sum_{j=1}^k \rho^{j-1} r_{t+j} = a + b^r \times (p_t-d_t)+\varepsilon^r \)
Then the 3 terms are
\( p_t - d_t = b^d \times (p_t-d_t) - b^r \times (p_t-d_t) + b^{pd} \times (p_t-d_t) \)
Yes, in that place are separate cherry-red together with bluish lines. Price-dividend ratios produce non forecast dividend increment hence the light-green draw is flat. Price dividend ratios produce forecast returns, simply plenty to draw organization human relationship for the volatility of prices.
Now, to the point: What if nosotros add together to a greater extent than variables to forecast returns together with dividend growth? Investors sure enough role lots of information. That would sure enough alter our agreement of the sources of cost volatility, no? In "Discount rates" I tried Lettau together with Ludvigson's cay variable. It did a slap-up labor of forecasting curt run returns. But it decays quickly, together with doesn't alter this long run painting present much at all.
Ok, but sure enough in that place are other variables out in that place that tin forecast returns together with dividend growth, that could upend the whole picture, no?
My exceed painting present answers that question. Even if you lot tin perfectly forecast returns, you lot volition non substantially alter the decomposition of price-dividend ratio volatility. The ex-post values are a form of upper saltation for how much things tin always change, no affair how much to a greater extent than data nosotros stick inwards the VAR. And the reply is, no affair how nosotros alter short-run furnish forecasts, no affair what data laid upwards nosotros use, the decomposition of cost volatility volition all the same tell the vast bulk of price-dividend ratio variation comes from expected returns. (And, likewise, Shiller's plots for ex-post dividends tell that no affair how many variables you lot try, dividend forecasts volition non explicate much price-dividend ratio volatility.)
You may either compassion or admire my MBAs who position upwards amongst this form of thing on a weekly basis. If you lot desire to a greater extent than details or documentation, it's problem laid upwards 3 here. Now, dorsum to writing Problem laid upwards 5.
One of the fun things almost pedagogy is that it forces me to facial expression dorsum at former ideas together with refine them. Last week, I needed a employment laid upwards for my MBA class. It occurred to me, why non convey them produce for returns what Shiller did for dividends?
Here it is
At each engagement \( t \) I plot the furnish together with lastly terms of the Campbell-Shiller identity
\( p_t - d_t = \sum_{\tau=t}^T \rho^{\tau-t-1} \Delta d_{\tau} - \sum_{\tau=t}^T \rho^{\tau-t-1} r_{\tau} + \rho^{T-\tau} \left( p_T-d_T \right) \)
where p = log price, d = log dividend, r = return, \(\rho = 0.96\)
In words, plot at each engagement the actual price-dividend ratio, the corresponding ex-post dividends, the corresponding ex-post return, together with ex-post terminal price. (There is no expectation on the correct manus side.) Shiller plots the price, dividend together with terminal cost term, (see here). I'm simply adding the furnish term.
Influenza A virus subtype H5N1 second, deeper, meaning. It is to a greater extent than conventional to brand this decomposition using expected values,
\( p_t - d_t = E_t \left[ \sum_{\tau=t}^T \rho^{\tau-t-1} \Delta d_{\tau} - \sum_{\tau=t}^T \rho^{\tau-t-1} r_{\tau} + \rho^{T-\tau} \left( p_T-d_T \right) \right] \)
For \(E_t\) nosotros role regression based forecasts, for example past times running long-run returns on dividend yields together with a vector of other variables. If you lot role dividend yields equally the forecasting variable together with hence each term is simply a break times dividend yield at fourth dimension t. To live specific, if you lot run
\( \sum_{j=1}^k \rho^{j-1} r_{t+j} = a + b^r \times (p_t-d_t)+\varepsilon^r \)
Then the 3 terms are
\( p_t - d_t = b^d \times (p_t-d_t) - b^r \times (p_t-d_t) + b^{pd} \times (p_t-d_t) \)
Since \(b^r \approx -1 \) (i.e. the regression coefficient of long run returns on d-p has a coefficient of almost +1) \( b^d \approx 0 , \ b^{pd}\approx 0 \) nosotros encounter that the discount charge per unit of measurement term accounts for all cost volatility. Plotting the terms is pretty boring:
Yes, in that place are separate cherry-red together with bluish lines. Price-dividend ratios produce non forecast dividend increment hence the light-green draw is flat. Price dividend ratios produce forecast returns, simply plenty to draw organization human relationship for the volatility of prices.
Now, to the point: What if nosotros add together to a greater extent than variables to forecast returns together with dividend growth? Investors sure enough role lots of information. That would sure enough alter our agreement of the sources of cost volatility, no? In "Discount rates" I tried Lettau together with Ludvigson's cay variable. It did a slap-up labor of forecasting curt run returns. But it decays quickly, together with doesn't alter this long run painting present much at all.
Ok, but sure enough in that place are other variables out in that place that tin forecast returns together with dividend growth, that could upend the whole picture, no?
My exceed painting present answers that question. Even if you lot tin perfectly forecast returns, you lot volition non substantially alter the decomposition of price-dividend ratio volatility. The ex-post values are a form of upper saltation for how much things tin always change, no affair how much to a greater extent than data nosotros stick inwards the VAR. And the reply is, no affair how nosotros alter short-run furnish forecasts, no affair what data laid upwards nosotros use, the decomposition of cost volatility volition all the same tell the vast bulk of price-dividend ratio variation comes from expected returns. (And, likewise, Shiller's plots for ex-post dividends tell that no affair how many variables you lot try, dividend forecasts volition non explicate much price-dividend ratio volatility.)
You may either compassion or admire my MBAs who position upwards amongst this form of thing on a weekly basis. If you lot desire to a greater extent than details or documentation, it's problem laid upwards 3 here. Now, dorsum to writing Problem laid upwards 5.




Post Comment
No comments